
NHKスペシャル
人類史上最大の数学の難問 「リーマン予想」 多くの数学者が挑戦しましたが敗れ、精神を病んでゆきました。
数学の世界に数ある難問、その中でも最も難しく、最も重要だと言われているのが今から150年前にドイツの天才数学者リーマンがこの世に送り出したリーマン予想という難問です。
リーマン予想がなぜ重要なのかそれは、数学の世界の最も基本となる素数の謎を解き明かすカギを握っているからなのです。
1と自分自身でしか割り切れない数 「素数」 は、数の原子とも呼ばれています。2から始まる不思議な数の列・・2・3・5・7・11・13・17・19・23・29・31・37・41・43・53・59・61・67・71・73・79・・・その並び方はバラバラでまったく規則は見当たりません。
しかしリーマン予想が証明されればこの気まぐれな素数の並びに何らかの大切な意味が隠されている事が明らかになるというのです。
それどころか素数は、大宇宙が従う自然法則に係る創造主の暗号ではないかと言われてもいるのです。
数学者ドン・ザギエ博士:「素数の列は、人間の知性を超えた存在であるように思えてなりません。素数にはこの自然の神秘を解き明かす何かが隠されているはずです」
数学者ブライアン・コンリー博士:「リーマン予想が証明できれば我々人類にとって一つの時代が終わり、新たな時代が始まる事を意味します。それは人類の知性の最高到達点となるでしょう」
この150年は、素数と言う魔性の難問に取りつかれた数学者たちの世紀を超えた闘いの歴史です。
古代ギリシャの昔から素数が無限に続く事は知られていました・・小学生でも知っている最も基本的な数、素数には世界の天才達をも悩ませる謎が隠されています。
1・2・3・4・5・6・7・8・・・無限に続く数の直線、注目していただきたいのが素数が現れるタイミング、実に気まぐれで不規則なんです・・素数が次々と現れるところもあれば、しばらく出てこない場所もあります。
現代数学者たちの究極の目標、それは気まぐれにしか見えない素数の並びにいったいどんな意味が隠されているのか・・いわばその暗号を解読する事です。
数学史上最大の難問、リーマン予想は、それを解き明かすための最も重要なステップなのです。
ちなみにリーマン予想(1859)は数学の言葉で 「ゼータ関数のい非自明なゼロ点はすべて一直線上にあるはずだ」 何が何だかさっぱりわかりませんよね。
ここからは、数学者が素数に挑んだ歴史です。
18世紀初めサンクトペテルブルグ(ロシア)の王宮に一人のスイス人数学者が招かれました。
当時ヨーロッパ№1の数学者レオンハルト・オイラー(1707~1783)です・・数学や物理学で数々の業績を残したオイラーが夢中になっていたのが素数の謎でした。

素数に取りつかれたオイラーは、ある奇妙な方法をとります・・「素数階段」です。・・素数に出会ったときだけ段が上がる階段です。
オイラーはこの奇妙な階段を頭の中で上り続けます・・10067・・31391・・実に72個も素数が現れない砂漠地帯もありました・・オイラーは上り続けます・・51203・・しかし素数の意味はわかりません。
素数に何らかの意味を見出そうとするオイラーに対し周囲は冷ややか
「素数が大自然と関係があると言うオイラー氏の考えは的外れだ」
「いったいこの世界のどこに素数があるのだ」
「素数は自然や宇宙とは関係ない無意味な数だ」
・・・と散々です。
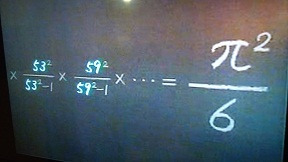
しかし批判を一気に吹き飛ばす発見をオイラーは成し遂げます。
オイラーは素数だけを使った風変わりな式を考えつきます・・この素数だけを使った式を計算すると・・なんと円周率を6で割ったものと等しくなったのです。
無秩序で決して美しくない素数だけの式が宇宙でも最も美しい形、円を現す円周率とつながっています。
そうです意味の無い存在だと思われていた素数の集まりが宇宙の究極の美の円を作り上げたのです。
オイラーは指数が単なる気まぐれの数ではなく宇宙の法則とつながっている可能性を初めて実証した人物となったのです。

オイラーの発見から100年が過ぎた19世紀の中ごろペルンハルト・リーマン(1826~1866)が数学史上最大の難問リーマン予想を世に送り出したのです。
リーマンは最新兵器 ”ゼータ関数” で闘いにいどみます。
リーマンはゼータ関数を立体的なグラフに描きます・・そしてグラフの高さがゼロになる 「ゼロ点」 となる点の位置を調べようと考えたのです。
ゼロ点はどこに現れるのか?・・当初の予想では、指数の並びが不規則なのだから素数の情報だけで作られたゼータ関数のゼロ点もバラバラに散らばってるはずでした。
しかし実際は、ゼロ点が一直線上に並んでいたのです。
「若しかしてまだ見つかっていない他のゼロ点も全て同じ直線状にあるのではないか」
このリーマンの直感こそが
リーマン予想(1859)「ゼータ関数のい非自明なゼロ点はすべて一直線上にあるはずだ」
・・・なのです。
リーマン予想がなにより画期的だったのは
「素数のい並びに意味はあるか?」
というそれまでの漠然とした問いを
「はすべてのゼロ点は一直線上にあるか?」
という数学の問題に焼き直した事でした。
これ以降、素数と言う暗号を解読しようという数学者たちのエネルギーはリーマン予想の証明に注がれる事になります。
しかしそれは、数学者たちの人生が次々に破壊されてゆく数奇な物語の始まりとなったのです。
リーマン予想に真っ向から挑む数学者が最初に現れたのは20世紀初頭のイギリスでした。
ゴッドフレイ・ハーディー
ジョン・リトルウッド
の二人がコンビを組んで発表した論文は100本、斬新な切り口が熱い称賛を呼び数学界に君臨します。
そして二人はリーマン予想に挑戦するのです・・ところがハーディー達はその後、最悪の挫折感を味わい続けるのです。
1914年ハーディーが発表した研究論文、この論文は当初リーマン予想を解決するものに思われました・・なぜならハーディーは、リーマンが予想したゼロ点が直線上に無限に存在する事を証明したからです。
しかしこの論文はリーマン予想の証明からはほど遠いものでした・・直線上以外にゼロ点が存在する可能性をつぶし切れていなかったのです。
「頂上にたどり着いたと思っていたら実は違う山に登っていた」
その後もリーマン予想は二人の挑戦を刎ねつけ続けたのです。
「リーマン予想は間違っている」
「正しいと言う証拠などない」
「予想が間違いであってくれさえすれば人生はずっと楽なのだ」
最強コンビの挫折は数学界に衝撃を与えました。

アメリカ プリンストン大学・・ここにリーマン予想の最大の犠牲者の一人、ジョン・ナッシュ博士がいます。
ノーベル経済賞の受賞者として知られるナッシュ博士は、1950年代世紀の天才と謳われた数学者でした。・・ナッシュ博士の型破りな天才ぶりは、アカデミー賞映画 「ビューティフル・マインド」 に描かれています。
そんな稀代の天才ナッシュが自らの能力の全てを懸けて挑む事になったのがリーマン予想でした。
「あのナッシュなら史上最大の難問を解いても不思議ではない」
ふくれあがる周囲の期待の中で博士は一人研究を続けます・・そしてリーマン予想について発表する講演会の日をむかえたのです。
「天才ナッシュは史上最大の難問を打ち砕いたに違いない」
満員の会場は期待します。
ところが打ち砕かれていたのは博士の精神の方だったのです。
「講演の途中で彼は突然たどたどしくなりました」
「言葉も支離滅裂でつじつまが合わない感じでした」
それは、その後30年以上に渡って博士を苦しめる事になる統合失調症の前兆でした。
この頃からリーマン予想は数学者のキャリアを一撃で破壊しかねない難問として恐れられるようになるのです。
素数の謎を解き明かす行為は神の怒りにふれるのではないかそんな言葉がささやかれるようになり、数学界全体がリーマン予想を敬遠する暗黒の時代に突入する事になったのです。

ここでチョット休憩
皆さんがインターネットでやり取りする商取引の個人情報を保護するのに一役買っているのが素数なんです。
その素数はスーパーコンピュータを駆使しても中々見つける事が出来ない150桁を超える巨大な素数(厳重な警備と金庫室で守られている)です。
なぜインターネットの情報を守るのに素数が使われるのか・・実は現代社会の通信の安全性は一般には決して知られる事がない巨大な素数を使った暗号によって守られているのです。
素数を使った暗号は、皆さんも日常で使っています・・キャッシュカードを機械に通した瞬間、ネットショップで購入ボタンをクリックした瞬間、巨大な素数が貴方のクレジット番号を瞬時に暗号化し、それを相手に安全に伝えているのです。
素数を使った暗号は、国家の機密情報、軍事情報のやり取りにも使われています。
もし素数の謎が全て明らかになり巨大な素数のリストが広く知られる事になれば現代社会の通信の安全性は大きく揺らぐのです。
素数を巡る数学者たちの挑戦と挫折は、私達の暮らしと決して無関係ではないのです。
1972年プリンストン高等研究所でおきた物理学者と数学者の偶然の出会いがそれまでリーマン予想を敬遠してきた数学者たちの空気を一変させます。
素粒子などミクロの世界を研究していた物理学の大御所フリーマン・ダイソン博士が息抜きにたってき
た午後3時のお茶の時間、たまたま訪れていた数学者ヒュー・モンゴメリー博士と何気ない会話をする事になるのです。
ダイソン:「何を研究してるって?」
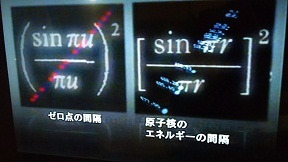
モンゴメリー:「こんな形の式(「ゼロ点」の間隔を表わす式)を研究してるのさ」
ダイソン:「え!その式は「原子核エネルギーの間隔」を表わす式とそっくりだ」
なんという偶然でしょう数学と原子学、物理学というまったく無関係の分野の二つの式がピタリと一致したのです。
この出会いの瞬間に起きた事を整理すると・・自然界の構成要素である原子、その中心に位置するのが原子核です。そのエネルギーは一定ではなく飛び飛びの値に変化するのが物理学者達の研究で明らかになっていました。
ダイソン博士の指摘は、この飛び飛びのエネルギーの間隔とゼロ点同士の間隔とに緊密な共通性があると言う事だったのです。
マーカス・デュ・トーソイ博士
「いったい誰が素数が原子核と一体であると予想できたでしょう。素数の謎を追い求めていた数学者は整数論の世界で研究を進め・・それとは関係なく原子核の謎を追っていた人は物理学の世界で研究を進めていたのです。ダイソンとモンゴメリーの出会いは突如としてこの二つの世界を融合させたのです」
いきなり表舞台に出たミクロの世界と素数とのつながり、この発見はリーマン予想を避けてきた数学者達の態度を大きく変える転機となりました。
1996年シアトルにて素数とリーマン予想について分野を超えて話し合う大会議が開かれました・・出席したのは世界を代表する数学者、物理学者など200人・・リーマン予想と自然法則とのつながりは、研究者達が共同して挑むべき人類にとって最も重要な挑戦だと位置づけられたのです。

会議では更に大きな進展がありました。
数学界最高の頭脳の一人 アラン・コンヌ博士 フィールズ賞にも輝いたこの天才数学者がリーマン予想解明につながる一つの道筋を見出したのです。
ミクロの空間に対する考え方の最新分野である 「非可換幾何学」 ならば大宇宙の成り立ちからミクロの世界まであらゆる現象を説明する究極の物理法則を人類が手に入れる為の基礎になるということです。
コンヌ博士が会議で気付いた事は、最新の幾何学が素数と極めて深い関係でつながっていると言う事実だったのです。
シアトルの会議以降、現在に至るまでコンヌ博士を初めとする数学者は素数の謎に迫ろうとする論文を次々と発表し始めたのです。
ある数学者は、「非可換幾何学」 を使って素数の謎が解けるとき宇宙のあらゆる現象を説明する万物の理論もまた完成するだろうと語っています。